Метод СИФ
В середине 80-х годов появился метод Систем Итерируемых Функций — СИФ (Iterated Function System — IFS) как простое средство получения фрактальных структур. Он был придуман американским математиком М. Барнсли (M. Barnsley), работавшим тогда в технологическом институте штата Джорджия. Сущность этого метода на примере уже упомянутой выше салфетки Серпинского заключается в следующем:
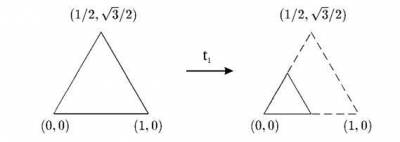
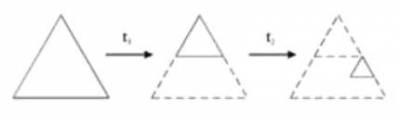
Поместим исходный равносторонний треугольник с длиной стороны, для определенности равной единице, на комплексную плоскость [z] так, как показано на рис. слева. Теперь зададимся вопросом, каким линейным преобразованием t1 на комплексной плоскости он переводится в равносторонний треугольник в два раза меньшего размера, показанный на рис.справа? Ответ достаточно прост. Поскольку левое основание обоих треугольников лежит в начале координат х = 0, то функция f1(z), осуществляющая это преобразование, определяется выражением:
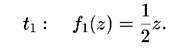
Если теперь сместить этот маленький треугольник по горизонтали вправо на величину, равную 1/2, то получим преобразование t2, переводящее исходный треугольник в треугольник, изображенный на рис. справа:
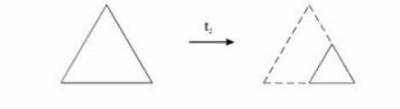
Соответствующая этому преобразованию функция f2(z) равна: 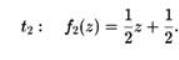
Наконец, последний, третий, маленький треугольник получается с помощью преобразования t3, показанного на рис.
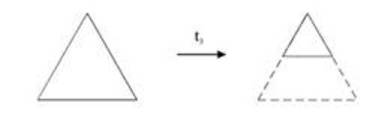
Отвечающая ему функция f3(z) получается из f1(z) трансляцией на комплексный вектор
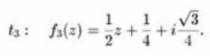
В итоге три вышеназванные линейные функции f1(z), f2(z), f3(z) осуществляют искомое преобразование исходного треугольника в три треугольника в два раза меньшего размера. Возникает вопрос, а что будет, если теперь каждый из этих трех маленьких треугольников в свою очередь подвергнуть этим трем преобразованиям. Тогда возникнет уже 9 треугольников с размером в 4 раза меньше исходного. Непосредственной проверкой можно убедиться, что это приводит к картинке, изображенной на рис. справа:
Например, выполняя сначала преобразование t3, а затем преобразование t2, мы в итоге получаем треугольник со стороной 1/4, показанный на предыдущем рис. справа, и т.д.. Здесь изображены все эти треугольники с обозначением результирующего преобразования — генеалогического кода, при помощи которого они были получены из исходного треугольника. Слева показан первый шаг итерационной процедуры. Большой треугольник, в который "вписаны" подобным образом три маленьких треугольника в два раза меньшего размера, мы будем ниже называть ячейкой.
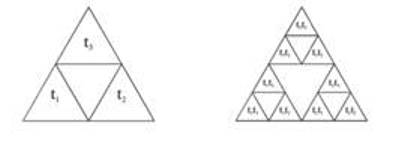
Комбинация tjti, стоящая в каждом из девяти маленьких треугольников, означает, что этот треугольник был получен из исходного сначала применением преобразования ti, а затем к полученному треугольнику было применено преобразование tj. Правило построения этой последовательности легко угадывается. На первом месте справа стоит первое преобразование. Оно соответствует позиции данного треугольника в его ячейке в соответствии с обозначениями на предыдущем рис. слева. На втором месте стоит второе по счету преобразование, которое соответствует позиции уже этого большого треугольника в его ячейке и т. д. Отметим очевидную некоммутативность двух (разных) преобразований, т.е. генеалогические коды (t1t2) и (t2t1) соответствуют разным треугольникам.
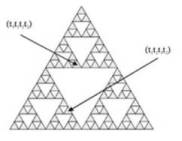
Ниже на рис. приведено 4-е поколение итераций, состоящее из 34= 81 треугольника, и показан генеалогический код двух из них. Ясно, что, действуя подобным образом, мы в точности воспроизводим алгоритм построения салфетки Серпинского. Поэтому после бесконечного числа шагов мы придем в конце концов к множеству точек, образующих этот фрактал.
С.В. Божокин, Д.А. Паршин "Фракталы и мультифракталы"
|
| Категория: Методы построения | Добавил: admin (03.04.2009)
|
| Просмотров: 2854
|
|
 |
| Форма входа |
|
 |
 |
| Поиск |
|
 |
 |
| Категории |
|
 |
 |
| гениально и просто |
|
 |
 |
| Counter |
|
 |
|