Классическое множество Кантора или пыль Кантора, названо по имени Георга Кантора, который описал его в 1883 году. Существование пыли кантора отмечалось до этого Генри Смитом в 1875 году или ещё ранее. Это множество известно как пример множества нулевой меры Лебега, чья мощность равна мощности континуума c.

Построение классической пыли Кантора начинается с выбрасыванием средней трети (не включая концы) единичного отрезка. То есть исходное множество есть отрезок [0,1], и первый шаг состоит в удалении открытого интервала (1/3, 2/3). На следующем и всех остальных шагах выкидываем среднюю треть (не включая концы) всех отрезков текущего уровня. Таким образом, получается последовательность множеств рис 1

.

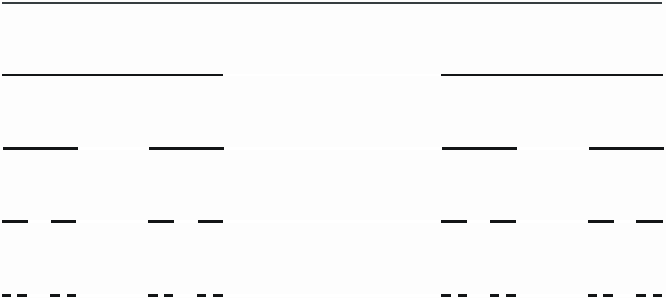
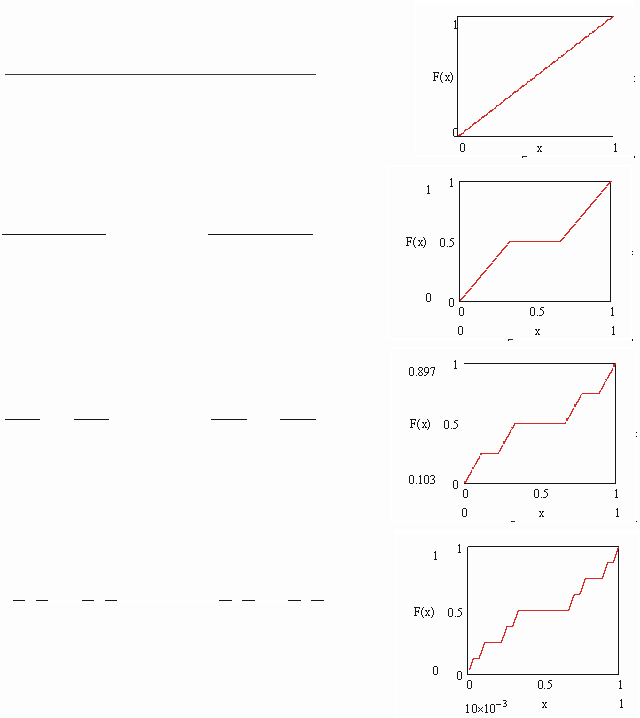
Рис.1

C₀ = [0, 1]

C₁ = [0, 1/3] È [2/3, 1]

C₂ = [0, 1/9] È [2/9, 1/3] È [8/9, 1]

…

C

Предельное множество C, которое представляет собой пересечение множеств C_n, n = 0, 1, 2, …, называется классическим множеством Кантора или пылью Кантора

Вычислим фрактальную размерность этого множества. Воспользуемся формулой (1). Очевидно, что на n-м шаге построения имеется 2ⁿ отрезков длины 1/3ⁿ каждый. Поэтому в качестве N(e ) на этом шаге можно взять величину 2ⁿ, а в качестве e — величину 1/3ⁿ. Предел e à 0 соответствует пределу n à ¥ . Поэтому фрактальная размерность равна

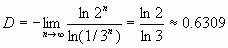
Она оказалась меньше Евклидовой размерности пространства, в котором располагается это множество (т.е. его длина равна нулю), но отлична от нуля, т.е. больше топологической размерности элементов (точек) этого множества.

Существует функциональный аналог множества Кантора — функция кантора. Распределим равномерно на C единичную массу (меру) с плотностью m . Тогда функция 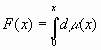описывает распределение меры на канторовом носителе. Она является непрерывной возрастающей функцией, которая тем не менее почти всюду имеет нулевую производную (т.е. горизонтальна). Её называют “чёртовой лестницей” (рис.2).