Определение фрактала

Каталог статей

Каталог файлов

Гениальное и безумное...

Обратная связь

О нас

Известные математики

Используемые источники

Допустим, что в результате первого броска выпала буква А. Со­единим мысленно нашу начальную точку с вершиной треугольника А отрезком прямой и на его середине поставим точку. Пусть теперь она будет играть роль начальной. После чего повторим вышеописанную процедуру с бросанием кубика и проставлением точ­ки в середине соответствующего отрезка. Допустим, на втором шаге выпала буква С, потом В, затем опять С и т. д. В результате на каж­дом шаге мы будем получать все новые и новые точки. Спрашивается, как распределятся внутри треугольника эти точки после достаточно большого числа шагов?

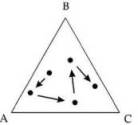
Ниже, (слева направо), показаны результаты этой игры соответственно с 5000, 10 ООО и 50 000 точек. Невероятно, но факт — по мере увеличения числа точек все явственнее проступает струк­тура треугольника Серпинского. Видно, что, хотя каждый раз выбор вершины треугольника происходит чисто случайным образом, возни­кающее множество точек на плоскости отнюдь не случайно и обладает ярко выраженной фрактальной структурой.

Связь этой простой игры в хаос с системой итерируемых функ­ций, рассмотренной в предыдущем параграфе, легко прослеживает­ся. Действительно, можно заметить, что по сути на каждом шаге к начальной точке г применялось (случайным образом выбранное) одно из трех вышеописанных линейных преобразований f₁(z), f₂(z) или f₃(z). Если обозначить координаты вершин треугольника А, В, С на комплексной плоскости через z_a, z_b,z_c  соответственно, то поскольку

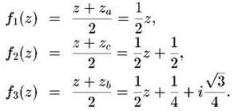                                                                            видно, что

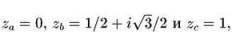
Таким образом, треугольник Серпинского, являясь аттрактором для этой системы итерируемых функций, возникает и при чисто случайном выборе последовательности преобразований t_i, t_j, t_k. Можно показать, что изображающая точка в результате бесконечной цепоч­ки случайных итераций сколь угодно близко подойдет к каждой точке этого фрактального множества поясняет эту мысль.

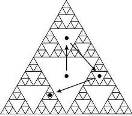
Разумеется, для этой игры было совершенно несущественно, что исходный треугольник являлся равносторонним. С равным успехом ее можно было провести в треугольнике любой формы.

А что будет, если мы теперь несколько изменим правила игры? Например, будем проставлять точку не на середине отрезка, а на расстоянии в 1/3 от соответствующей вершины. Результат показан на ниже. Получившееся множество точек можно назвать дву­мерным аналогом канторовского множества исключенных средних третей. Нетрудно подсчитать, что фрактальная размерность соот­ветствующего аттрактора равна единице

В качестве исходной фигуры можно выбрать и любой другой мно­гоугольник. Например, квадрат. Однако в случае квадрата нас ожи­дает сюрприз. Если проводить игру по тем же правилам, что и для треугольника Серпинского (т. е. ставить новую точку на середине отрезка), то точки равномерно заполнят весь квадрат (подумайте, почему?).  Но если, например, взять правильный шестиугольник и ставить точку не в середине отрезка, а на расстоянии в 1/3 от со­ответствующей вершины, то эти точки в процессе итераций образу­ют множество, которое условно можно назвать шестиугольником Серпинского. Он показан на рис.  

так видно, он состоит из о одинаковых частей, каждая из которых подобна целому, но имеет размер в три раза меньше исходного. По­этому его фрактальная размерность D=ln6/ln3=1.6309. Кстати, именно в этом случае игра в хаос будет настоящей игрой в кости, так как теперь на шести гранях игрального кубика можно поставить цифры от одного до шести, соответствующие каждой из вершин шес­тиугольника. Заметьте также, что внутренняя граница этой фигуры представляет собой нам уже известный фрактал — снежинку Коха (см. рис. 1.3).

Систему итерируемых функций для этой и ей подобных задач лег­ко написать в общем виде, пользуясь заданными алгоритмами игры.

Так, для произвольного n-угольника в случае, когда следующая точка ставится на расстоянии в l/т от соответствующей вершины, где / — расстояние до нее начальной точки, am — некоторое (не обязательно целое) число, превышающее единицу, эта система имеет вид

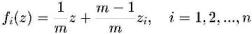
Здесь z1 — комплексные координаты вершин многоугольника. На­пример, для п = 2 (z=0 ,z = 1) и т = 3 получаем СИФ для уже известного канторовского множества исключенных средних третей.